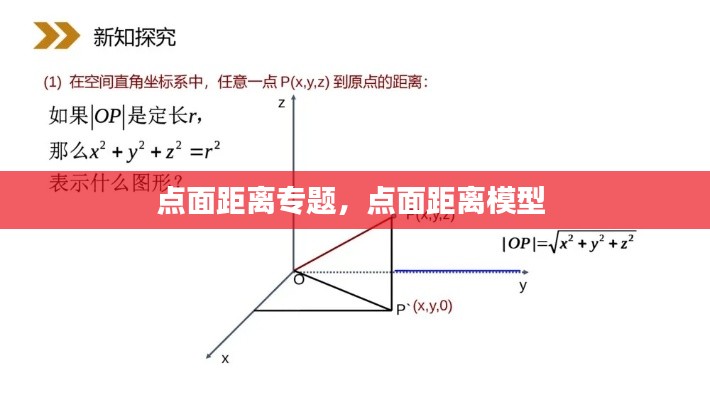
什么是点面距离

点面距离，顾名思义，是指从一个点到另一个面的最短距离。在几何学中，这个概念广泛应用于空间几何、立体几何等领域。点面距离的计算方法有多种，根据具体情况选择合适的方法至关重要。

点面距离的计算方法

点面距离的计算通常有三种方法：解析法、向量法和坐标法。

1. 解析法：通过建立点与面的方程，求解方程组得到点面距离。这种方法适用于点与面方程已知的情况。

2. 向量法：利用向量的性质，通过计算向量之间的夹角和模长来求解点面距离。这种方法适用于点与面方程未知，但知道点与面的关系时。

3. 坐标法：通过坐标变换，将点面距离问题转化为平面几何问题求解。这种方法适用于点与面坐标已知的情况。

点面距离的应用实例

点面距离在现实生活中的应用非常广泛，以下列举几个实例：

1. 地理信息系统（GIS）：在GIS中，点面距离可以用于计算两点之间的最短路径，为城市规划、交通导航等提供数据支持。

2. 机器人导航：在机器人导航系统中，点面距离可以帮助机器人避开障碍物，实现自主导航。

3. 工程测量：在工程测量中，点面距离可以用于计算地形高程，为工程建设提供依据。

点面距离在计算机图形学中的应用

在计算机图形学中，点面距离的应用同样具有重要意义。以下列举几个应用场景：

1. 视觉化：通过计算点面距离，可以生成三维场景的视觉效果，如虚拟现实（VR）和增强现实（AR）技术。

2. 光照模型：在光照模型中，点面距离可以用于计算光照强度，影响物体的渲染效果。

3. 碰撞检测：在游戏开发中，点面距离可以用于检测物体之间的碰撞，实现物理效果。

点面距离的优化算法

随着计算机技术的发展，点面距离的计算方法也在不断优化。以下介绍几种常见的优化算法：

1. 二分查找法：通过不断缩小搜索范围，找到点面距离的最小值。适用于点面距离在较大范围内求解的情况。

2. 最小二乘法：通过最小化误差平方和，求解点面距离。适用于点面距离存在误差的情况。

3. 改进遗传算法：利用遗传算法搜索最优解，提高点面距离计算的精度。适用于点面距离求解复杂、计算量大且精度要求高的场景。

总结

点面距离是几何学中一个重要的概念，其在各个领域的应用日益广泛。掌握点面距离的计算方法及其应用，有助于我们更好地理解和解决实际问题。随着技术的不断发展，点面距离的计算方法也在不断优化，为各个领域的发展提供了有力支持。